Description

Given a string s containing just the characters '(', ')', '{', '}', '[' and ']', determine if the input string is valid.

An input string is valid if:

• Open brackets must be closed by the same type of brackets.
• Open brackets must be closed in the correct order.
• Every close bracket has a corresponding open bracket of the same type.

Examples

• Example 1:
  • Input: s = "()"
  • Output: true
• Example 2:
  • Input: s = "()[]{}"
  • Output: true
• Example 3:
  • Input: s = "(]"
  • Output: false
• Example 4:
  • Input: s = "([])"
  • Output: true

Constraints

• 1 <= s.length <= 10⁴
• s consists of parentheses only '()[]{}'.

Test

fn main() {
    assert_eq!(Solution::is_valid(String::from("()")), true);
    assert_eq!(Solution::is_valid(String::from("()[]{}")), true);
    assert_eq!(Solution::is_valid(String::from("([])")), true);
    assert_eq!(Solution::is_valid(String::from("(]")), false);
    assert_eq!(Solution::is_valid(String::from("(")), false);
    assert_eq!(Solution::is_valid(String::from("())")), false);
    assert_eq!(Solution::is_valid(String::from("))(")), false);

    assert_eq!(Solution::is_valid(String::from("[]")), true);
    assert_eq!(Solution::is_valid(String::from("{}")), true);
    assert_eq!(Solution::is_valid(String::from("[({})]")), true);
    assert_eq!(Solution::is_valid(String::from("({[()]})")), true);
    assert_eq!(Solution::is_valid(String::from("([)]")), false);
    assert_eq!(Solution::is_valid(String::from("(()))")), false);
    assert_eq!(Solution::is_valid(String::from("((()")), false);
    assert_eq!(Solution::is_valid(String::from("){")), false);
    assert_eq!(Solution::is_valid(String::from("{[}]}")), false);
}

Prototype

pub fn is_valid(s: String) -> bool {
    todo!()
}

Solutions

Brute force

We can break the problem into smaller parts. Essentially, the parentheses are valid only when each opening symbol is immediately followed by its corresponding closing symbol (e.g., (), {}, []). In our loop, we check if the string contains any of these sequences and remove them. If the string becomes empty after all removals, the parentheses are valid; otherwise, they are not.

// we can modify the given argument to be mutable
pub fn is_valid(mut s: String) -> bool {
    while s.contains("{}") || s.contains("[]") || s.contains("()") {
        s = s.replace("{}", "");
        s = s.replace("()", "");
        s = s.replace("[]", "");
    }
    s.is_empty()
}

• Time Complexity: O(n²)
• Space Complexity: O(n)

Stack

The stack solution allows us to solve the problem in a single iteration over the given string. Essentially, we store our opening characters on a stack, and when we encounter a closing character, we compare it with the top of the stack. If they match, we pop the stack; otherwise, the string is invalid.

Valid example

Let’s consider a valid example: "({})".

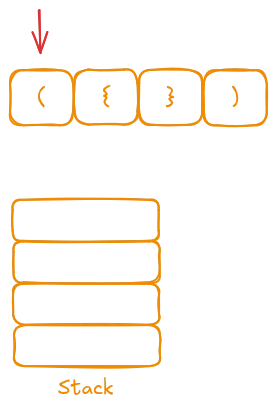
We start the iteration with the "(" symbol. Since it’s an opening character, we push it onto the stack.

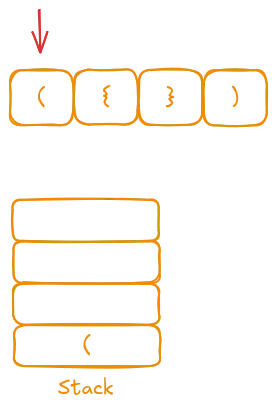
Next, we encounter "{", which is also an opening character, so we push it onto the stack.

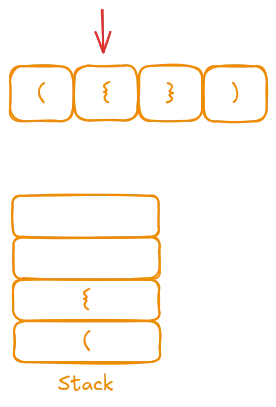
Now, we encounter a closing character "}". We compare it with the top of the stack. Since the top is "{", they match, so we pop the stack.

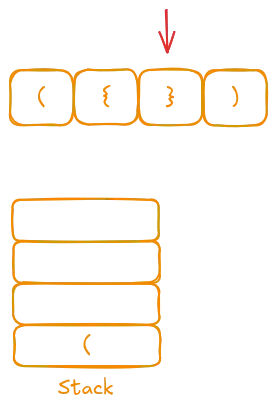
Finally, we encounter ")". The top of the stack is "(", so we pop it. The iteration is complete and our stack is empty, which means the string is valid.

Not valid examples and edge cases

Example 1

We can try "(]". We start with the opening "(", we push it onto the stack.

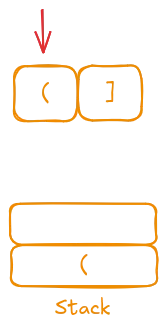
The next character is a closing "]". We compare it with the top of the stack where we store the opening characters in reverse order. It is "(", and it doesn’t match. The string is not valid.

Example 2

The string value is "]".

The current character is "]". We compare it with the top of the stack, but the stack is empty—this is an edge case that should be handled.

Implementation

pub fn is_valid(s: String) -> bool {
    let mut stack: Vec<char> = Vec::new();

    for current_char in s.chars() {
        match (stack.last(), current_char) {
            // If the stack is empty (the last stack element is None)
            //or the current character is an opening symbol, push it onto the stack.
            (None, _) | (_, '{') | (_, '(') | (_, '[') => stack.push(current_char),
            // If the top of the stack is the matching opening symbol
            // for the current closing symbol, pop it.
            (Some('{'), '}') | (Some('('), ')') | (Some('['), ']') => {
                stack.pop();
            }
            // Otherwise, the string is invalid.
            _ => return false,
        }
    }
    // String is valid when there are no more chars on stack
    stack.is_empty()
}

• Time Complexity: O(n)
• Space Complexity: O(n)