Top K Frequent Elements

347. Top K Frequent Elements

Arrays & Hashing

Array, Hash Table, Devide and Conquer, Sorting, Heap (Priority Queue), Bucket Sort, Counting, Quick select

Medium

Description

Given an integer array nums and an integer k, return the k most frequent elements. You may return the answer in any order.

Examples

Example 1:
- Input: nums = [1,1,1,2,2,3], k = 2
- Output: [1,2]
Example 4:
- Input: nums = [1], k = 1
- Output: [1]

Constraints

1 <= nums.length <= 10⁵
-10⁴ <= nums[i] <= 10⁴
k is in the range [1, the number of unique elements in the array].
It is guaranteed that the answer is unique.

Follow up: Your algorithm’s time complexity must be better than O(n log n), where n is the array’s size.

Test

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn test_example1() {
        let nums = vec![1, 1, 1, 2, 2, 3];
        let k = 2;
        let mut result = top_k_frequent(nums, k);
        result.sort();
        let mut expected = vec![1, 2];
        expected.sort();
        assert_eq!(result, expected);
    }

    #[test]
    fn test_example2() {
        let nums = vec![1];
        let k = 1;
        let result = top_k_frequent(nums, k);
        let expected = vec![1];
        assert_eq!(result, expected);
    }

    #[test]
    fn test_empty_input() {
        let nums: Vec<i32> = vec![];
        let k = 0;
        let result = top_k_frequent(nums, k);
        let expected: Vec<i32> = vec![];
        assert_eq!(result, expected);
    }

    #[test]
    fn test_all_same_elements() {
        let nums = vec![4, 4, 4, 4];
        let k = 1;
        let result = top_k_frequent(nums, k);
        let expected = vec![4];
        assert_eq!(result, expected);
    }

    #[test]
    fn test_more_frequent_elements_than_k() {
        let nums = vec![1, 1, 2, 2, 3, 3, 3, 4, 4, 5];
        let k = 2;
        let result = top_k_frequent(nums, k);
        // The two most frequent elements are 3 and (1,2, or 4); order may vary.
        // We ensure that 3 is always present.
        assert!(result.contains(&3));
        // Also check that the result length is k.
        assert_eq!(result.len(), k as usize);
    }
}

Prototype

pub fn top_k_frequent(nums: Vec<i32>, k: i32) -> Vec<i32> {
    todo!()
}

Solutions

We face several challenges in this problem. First, we need to count the occurrences of each number, and a hash map is an excellent data structure for storing a number as a key along with its occurrence count. We will use it in both solutions.

The second challenge is how to transform this hash map into the final result, and this part differs between solutions.

Another important condition, that we can return same counts in any order! For example if k is 1 and top frequent are 2, 3, 4 we can return any number.

Function Skeleton:

pub fn top_k_frequent(nums: Vec<i32>, k: i32) -> Vec<i32> {
    let mut counts: HashMap<i32, usize> = HashMap::new();

    // Count how many times each number occurs.
    for num in nums {
        *counts.entry(num).or_insert(0) += 1;
    }
    todo!()
}

Sorting

Since we already have our hash map with counts, we can sort these occurrence counts without losing track of which number they belong to. In this solution, we transform the initial vector several times:

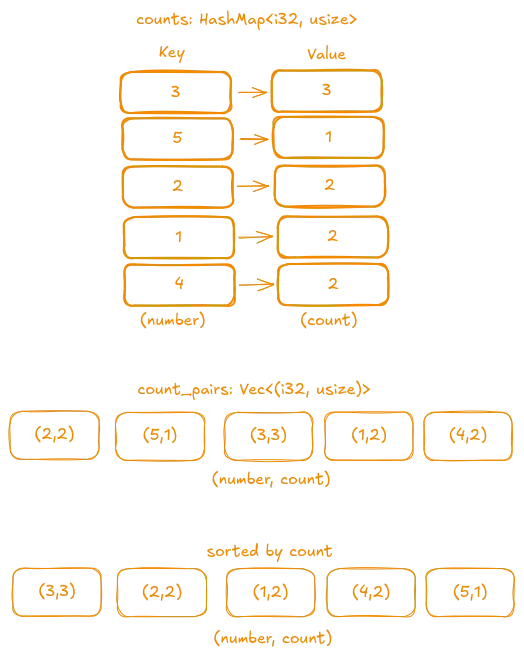
Step 1: Convert our hash map into a vector of tuples, where one element is the number and the other is its occurrence count.
Step 2: Sort the vector by counts in decreasing order.
Step 3: After sorting, take only the top k elements and extract the numbers.

For example, consider vec![1, 1, 2, 2, 3, 3, 3, 4, 4, 5] to see how the mapping will look at different stages.

Sorting

pub fn top_k_frequent(nums: Vec<i32>, k: i32) -> Vec<i32> {
    let mut counts: HashMap<i32, usize> = HashMap::new();

    // Count how many times each number occurs.
    for num in nums {
        *counts.entry(num).or_insert(0) += 1;
    }

    // Convert the hash map to a vector of tuples (number, count).
    let mut count_pairs = counts.into_iter().collect::<Vec<_>>();
    // Sort the vector by counts in decreasing order.
    count_pairs.sort_by(|(_, count1), (_, count2)| count2.cmp(count1));
    // Extract only the numbers from the top k elements.
    count_pairs
        .into_iter()
        .map(|(val, _)| val)
        .take(k as usize)
        .collect()
}

Time Complexity: O(n log n)
Space Complexity: O(n)

Bucket Sort

The other approach is to use bucket sort. For this method, we represent our buckets as a vector where the index represents the count and the value is a list of numbers. We use the index as the count because we know that the maximum count is initial vector size + 1, and the buckets will be naturally ordered. We use a vector for the values because multiple numbers can occur the same number of times.

For example, consider vec![1, 1, 2, 2, 3, 3, 3, 4, 4, 5] to see how the mapping will look at different stages.

Buckets

pub fn top_k_frequent(nums: Vec<i32>, k: i32) -> Vec<i32> {
    let mut counts: HashMap<i32, usize> = HashMap::new();
    let mut buckets = vec![vec![]; nums.len() + 1];

    // Count how many times each number occurs.
    for num in nums {
        *counts.entry(num).or_insert(0) += 1;
    }

    // Push each number into the corresponding bucket.
    for (num, count) in counts {
        buckets[count].push(num);
    }

    buckets
        .into_iter()
        // Flatten the buckets into a single iterator.
        .flatten()
        // Reverse to start from the most frequent numbers.
        .rev()
        // Take only k elements.
        .take(k as usize)
        .collect()
}

Time Complexity: O(n)
Space Complexity: O(n)