Description

Given an array of integers temperatures represents the daily temperatures, return an array answer such that answer[i] is the number of days you have to wait after the ith day to get a warmer temperature. If there is no future day for which this is possible, keep answer[i] == 0 instead.

Examples

• Example 1:

  • Input: temperatures = [73,74,75,71,69,72,76,73]
  • Output: [1,1,4,2,1,1,0,0]

• Example 2:

  • Input: temperatures = [30,40,50,60]
  • Output: [1,1,1,0]

• Example 3:

  • Input: temperatures = [30,60,90]
  • Output: [1,1,0]

Constraints

• 1 <= temperatures.length <= 10⁵
• 30 <= temperatures[i] <= 100

Test

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn test_example1() {
        let temperatures = vec![73, 74, 75, 71, 69, 72, 76, 73];
        let result = daily_temperatures(temperatures);
        let expected = vec![1, 1, 4, 2, 1, 1, 0, 0];
        assert_eq!(result, expected);
    }

    #[test]
    fn test_example2() {
        let temperatures = vec![30, 40, 50, 60];
        let result = daily_temperatures(temperatures);
        let expected = vec![1, 1, 1, 0];
        assert_eq!(result, expected);
    }

    #[test]
    fn test_example3() {
        let temperatures = vec![30, 60, 90];
        let result = daily_temperatures(temperatures);
        let expected = vec![1, 1, 0];
        assert_eq!(result, expected);
    }

    #[test]
    fn test_single_element() {
        let temperatures = vec![50];
        let result = daily_temperatures(temperatures);
        let expected = vec![0];
        assert_eq!(result, expected);
    }

    #[test]
    fn test_descending_order() {
        let temperatures = vec![100, 90, 80, 70];
        let result = daily_temperatures(temperatures);
        let expected = vec![0, 0, 0, 0];
        assert_eq!(result, expected);
    }

    #[test]
    fn test_all_same() {
        let temperatures = vec![50, 50, 50, 50];
        let result = daily_temperatures(temperatures);
        let expected = vec![0, 0, 0, 0];
        assert_eq!(result, expected);
    }
}

Prototype

pub fn daily_temperatures(temperatures: Vec<i32>) -> Vec<i32> {
    todo!()
}

Solutions

Brute Force

The brute force solution is, as always, not very efficient—one test may even fail with a timeout. We can “trick” this test because it contains many duplicates, but let’s not spend too much time on that. The idea is simple: we use nested loops to iterate until we find a number greater than the current one.

pub fn daily_temperatures(temperatures: Vec<i32>) -> Vec<i32> {
    let mut res = vec![0; temperatures.len()];
    for (i, &num) in temperatures.iter().enumerate() {
        for y in i..temperatures.len() {
            if temperatures[y] > num {
                res[i] = (y - i) as i32;
                break;
            }
        }
    }
    res
}

• Time Complexity: O(n²)
• Space Complexity: O(n)

Stack

The stack solution is straightforward to implement. Let’s start with an example:

• Input: temperatures = [73,74,75,71,69,72,76,73]
• Output: [1,1,4,2,1,1,0,0]

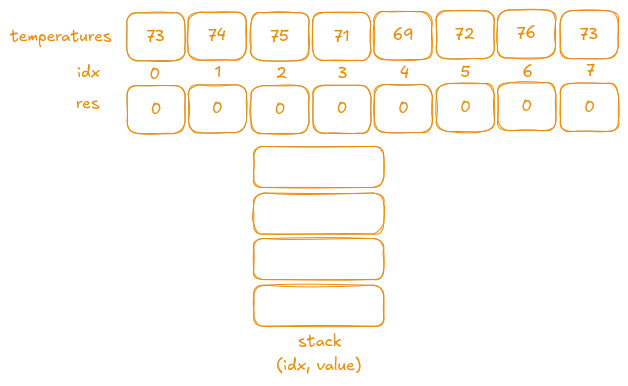
First, we initialize the res vector with all zeroes as a default value when no higher temperature is found. With a stack, we push a tuple (index, temperature) onto it, and whenever we encounter a temperature greater than the one at the top of the stack, we pop from the stack.

There are a couple of challenges to note:

• Index Difference:
  Each value in the output represents the difference in indexes between the current temperature and the next higher temperature. Therefore, we need to keep track of the indexes by using a tuple (index, value).

• Multiple Elements on the Stack:
  In some cases, there may be multiple elements on the stack waiting for a higher temperature. Our solution should handle these scenarios appropriately.

Let’s walk through the iteration:

1. Iteration 1:
   The first value is 73. Since the stack is empty, we push (0, 73) onto the stack.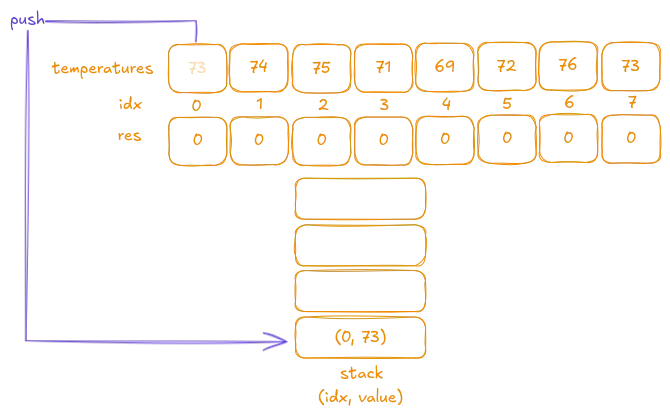

   

2. Iteration 2:
   The next value is 74, which is greater than the temperature at the top of the stack (73).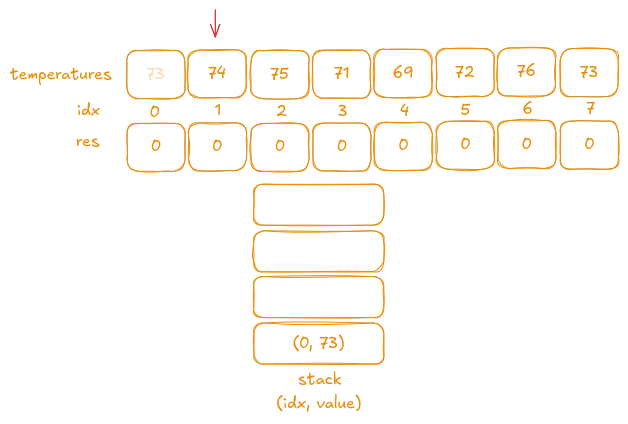

   

   We pop the tuple (0, 73) from the stack. The difference in indexes is 1 - 0 = 1, so we set res[0] to 1. And then we push the current temperature[i] onto stack to find a higher value for it as well.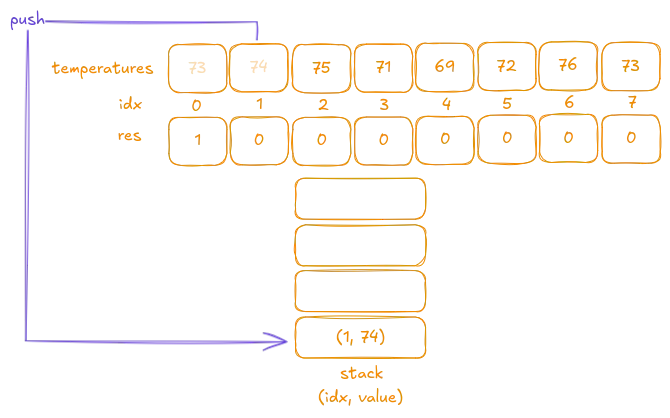

   

3. Iteration 3:
   The next value is 75, which is greater than the current stack top 74. We follow the same steps as before: pop the top element, calculate the difference in indexes, and update the result.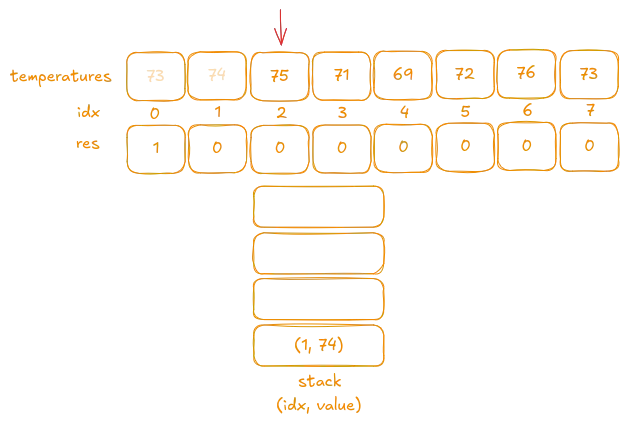

   
   

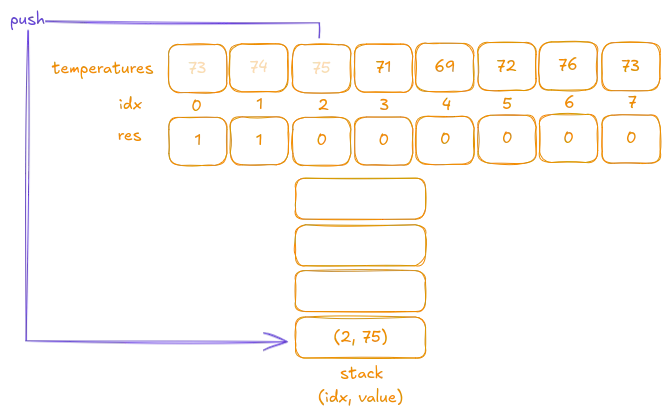
4. Iteration 4 & 5:
   I’ll combine the next two iterations because the same action is performed in both. Consider the next two values: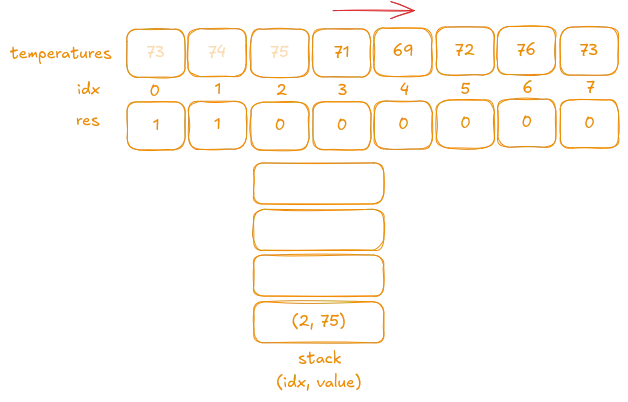

   

   As shown, the next value 71 is less than the current stack top 75, so we push it onto the stack. Then, the following value 69 is less than the new stack top 71, so it is also pushed onto the stack.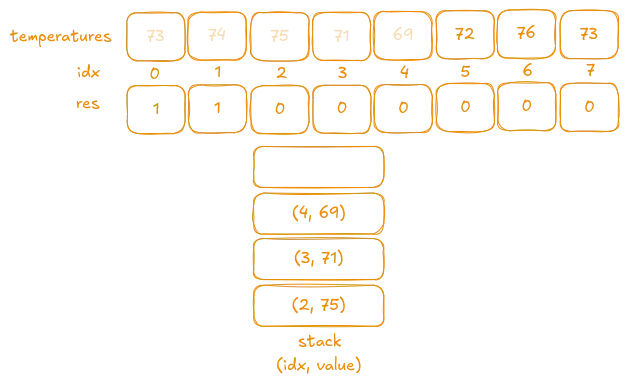

   

   FYI: On the stack, we now see (from top to bottom): 69, 71, 75. This structure is called a Monotonic Decreasing Stack.

5. Iteration 6:
   The next value is 72, which is greater than the top of the stack 69. We pop the tuple (4, 69). The current index is 5, so we update res[4] to 5 - 4.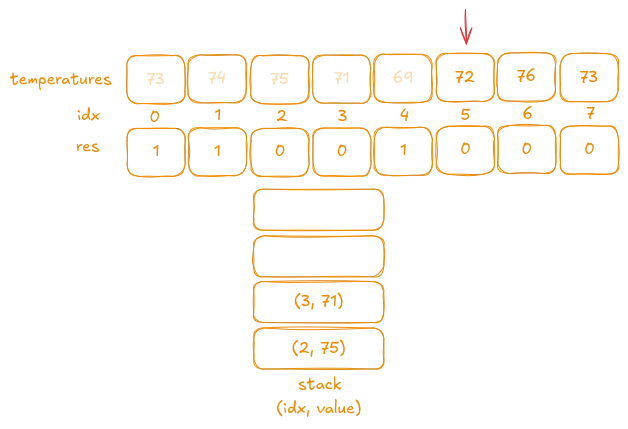

   

   Since 69 has been popped, the new stack top is 71, and 72 is greater than 71 as well. To handle temperatures that are higher after more than one day, we continue to pop elements while the current value exceeds the stack top.

   Next, we pop the tuple (3, 71). The current index is still 5, so we update res[3] to 5 - 3.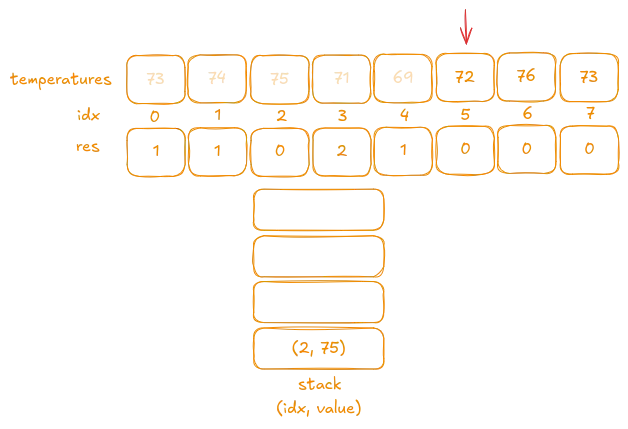

   

   We can handle now all cases.

pub fn daily_temperatures(temperatures: Vec<i32>) -> Vec<i32> {
    let mut res = vec![0; temperatures.len()];
    let mut stack: Vec<(usize, i32)> = vec![];

    for (i, cur_temp) in temperatures.into_iter().enumerate() {
        while let Some(&(top_stack_idx, top_stack_val)) = stack.last() {
            if cur_temp > top_stack_val {
                res[top_stack_idx] = (i - top_stack_idx) as i32;
                stack.pop();
            } else {
                break;
            }
        }
        stack.push((i, cur_temp))
    }
    res
}

• Time Complexity: O(n)
• Space Complexity: O(n)